Máy học phổ thông (3) | Python Cho Người Việt

Trong phần 1, chúng ta đã xem xét một phương pháp hồi quy đơn giản. Trong phần này chúng ta sẽ xem xét một phương pháp hồi quy khác có tên hồi quy hậu cần (logistic regression).

Hàm hậu cần và hàm xích-ma chuẩn

Hàm hậu cần (logistic function)

Năm 1845, nhà toán học Bỉ tên Pierre François Verhulst đăng bài "Những nghiên cứu toán học về quy luật của sự phát triển dân số". Trong đó, ông đặt tên cho hàm có đồ thị chữ S (đường cong xích-ma) và công thức như sau là hàm hậu cần:

\begin{equation*} f(x) = \cfrac{L}{1 + e^{-k(x-x_0)}} \end{equation*}

với:

\(x_0\) là giá trị trục hoành ở trung điểm của hàm
\(L\) là giá trị cực đại của hàm
\(k\) là độ dốc của hàm

Ví dụ, với \(L=1, k=1, x_0=0\), hàm hậu cần đặc biệt này là hàm xích-ma chuẩn có đồ thị như sau:

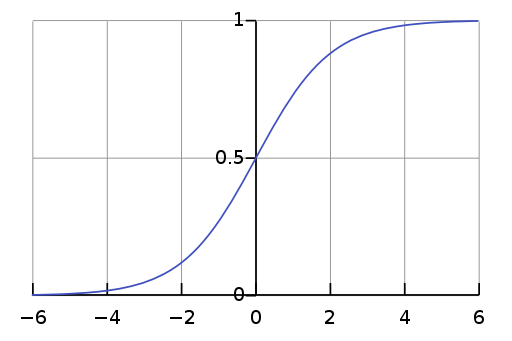
Đồ thị hàm xích-ma chuẩn (bởi Qef [Public domain], nguồn Wikimedia Commons)

Nhìn vào đồ thị, ta thấy rằng khi dân số bắt đầu tăng thì sự tăng trưởng này dường như theo cấp lũy thừa, rồi sau đó khi gần bão hòa thì sự tăng trưởng giảm lại, và đến cuối cùng thì sự tăng dân số gần như dừng hẳn. Tốc độ sinh sản tỷ lệ với cả số dân hiện tại và lượng tài nguyên có sẵn. Đó là lý do tại sao hàm này có tên là hàm hậu cần.

Hàm xích-ma chuẩn (standard sigmoid function)

Chúng ta đã đề cập đến hàm xích-ma chuẩn trong mục trên. Mục này sẽ nêu ra một vài nhận xét quan trọng. Và từ bây giờ, khi nói đến hàm xích-ma, ta nói đến hàm xích-ma chuẩn này.

Trước tiên, ta sẽ viết lại hàm xích-ma theo dạng một hàm hậu cần với các giá trị thích hợp.

\begin{equation*} S(x) = \cfrac{1}{1 + e^{-x}} \end{equation*}

Hàm xích-ma có giá trị trong khoảng \((0, 1)\). Tức là hàm này bị chặn trên bởi tiệm cận \(y = 1\) và chặn dưới bởi tiệm cận \(y = 0\).
Hàm xích-ma hoàn toàn đối xứng qua trung điểm tại \(x_0 = 0\), hay \(S(-x) = 1 - S(x)\).
Hàm xích-ma có đạo hàm (khả vi) ở mọi điểm.

Từ hai nhận xét đầu, ta thấy rằng giá trị của hàm xích-ma rất có thể được dùng để biểu diễn một xác suất của biến nhị phân nào đấy. Nhận xét cuối khiến ta nghĩ đến kỹ thuật xuống dốc.

Đạo hàm của hàm xích-ma chuẩn có thể tìm được như sau:

\begin{align*} S^\prime(x) &= \cfrac{\partial}{\partial x} \left( \cfrac{1}{1 + e^{-x}} \right) \\ &= \cfrac{1}{(1 + e^{-x})^2} (e^{-x}) \\ &= \cfrac{1}{1 + e^{-x}} \cfrac{e^{-x}}{1 + e^{-x}} \\ &= \cfrac{1}{1 + e^{-x}} \times \left( 1 - \cfrac{1}{1 + e^{-x}} \right) \\ &= S(x)(1 - S(x)) \end{align*}

Hồi quy hậu cần (logistic regression)

Phương pháp hồi quy hậu cần

Trong phương pháp hồi quy tuyến tính, quan hệ giữa biến phụ thuộc và biến độc lập được giả định là quan hệ tuyến tính. Tương tự, hồi quy hậu cần giả định mối quan hệ này là một hàm hậu cần, cụ thể là hàm xích-ma chuẩn.

Giả sử các biến độc lập \(x_1, \dots, x_n\) cùng với \(x_0 = 1\) được viết dưới dạng véc tơ là \(\vec{x}\), và tham số của mô hình hồi quy \(\theta_0, \theta_1, \dots, \theta_n\) cũng được viết dưới dạng véc tơ là \(\vec{\theta}\), phương pháp hồi quy hậu cần trong bài này giả định rằng:

\begin{equation*} \hat{y} = S(\vec{\theta} \cdot \vec{x}) \end{equation*}

Ký hiệu \(\vec{a} \cdot \vec{b}\) thể hiện tích vô hướng (dot product) của hai véc tơ. Tích vô hướng này có giá trị là tổng của tích của các cặp phần tử tương ứng, \(\sum_i a_i \times b_i\).

So với hồi quy tuyến tính \(\hat{y} = \vec{\theta} \cdot \vec{x}\), ta nhận thấy rằng hồi quy hậu cần chỉ thêm ở chỗ tính giá trị của hàm xích-ma từ tích vô hướng.

Ví dụ hàm AND

Giả sử chúng ta có bảng dữ liệu đầu vào như sau:

Dòng	\(x_1\)	\(x_2\)	\(y\)
0	0	0	0
1	0	1	0
2	1	0	0
3	1	1	1

Bảng dữ liệu này thể hiện giá trị thực (actual value) của cổng AND. Nếu vẽ đồ thị 2 chiều ta sẽ có hình như sau (màu đỏ thể hiện giá trị \(y = 0\) và màu xanh lá cây thể hiện giá trị \(y = 1\)):

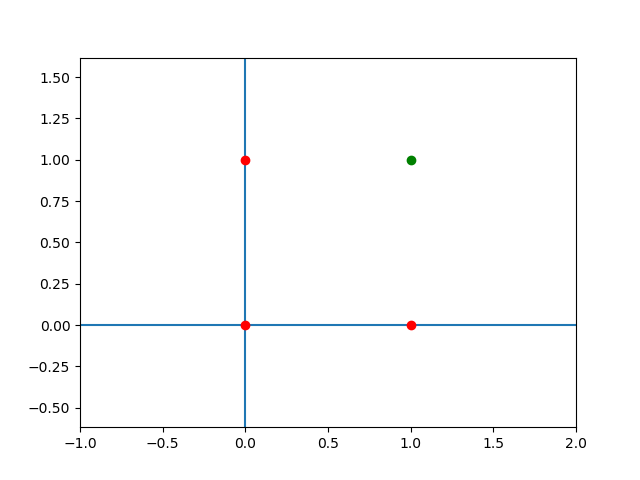
Giá trị thực của cổng AND

# encoding: utf-8
from matplotlib import pyplot as plt

plt.axes().set_aspect('equal', 'datalim')
plt.axvline(x=0)
plt.axhline(y=0)
plt.xlim(-1, 2)
plt.ylim(-1, 2)
plt.plot([0, 0, 1], [0, 1, 0], 'ro')
plt.plot([1], [1], 'go')
plt.savefig('logistic-regression-1.png')

Điểm quan trọng của bảng dữ liệu đầu vào này là giá trị của biến \(y\) chỉ có hai khả năng, hoặc là \(0\), hoặc là \(1\).

Xác lập hàm mất mát từ sai số

Gọi \(erf_\vec{\theta}(\vec{x}, y)\) là sai số của mô hình khi tham số là \(\vec{\theta}\), dữ liệu đầu vào là véc tơ \(\vec{x}\) và giá trị thực là \(y\). Vì giá trị dự đoán \(\hat{y}\) bị chặn trong khoảng \((0, 1)\) nên với mỗi dòng, sai số (không âm) sẽ là:

\begin{align*} erf_\vec{\theta}(\vec{x}, y) & = \begin{cases} 1 - \hat{y} & \mbox{khi } y = 1 \\ \hat{y} - 0 & \mbox{khi } y = 0 \end{cases} \\ & = \begin{cases} 1 - S(\vec{\theta} \cdot \vec{x}) & \mbox{khi } y = 1 \\ S(\vec{\theta} \cdot \vec{x}) - 0 & \mbox{khi } y = 0 \end{cases} \end{align*}

Với một chút sáng tạo, chúng ta có thể gộp hai điều kiện này lại như sau:

\begin{align*} erf_\vec{\theta}(\vec{x}, y) = & y \times \left( 1 - S(\vec{\theta} \cdot \vec{x}) \right) + (1 - y) \times S(\vec{\theta} \cdot \vec{x}) \\ = & y + (1 - 2y) \times S(\vec{\theta} \cdot \vec{x}) \end{align*}

Theo thói quen, chúng ta sẽ lấy đạo hàm bậc nhất (để áp dụng kỹ thuật xuống dốc nhằm tìm điểm cực tiểu của \(erf\).

\begin{align*} \cfrac{\partial}{\partial \vec{\theta}} erf_\vec{\theta}(\vec{x}, y) & = \cfrac{\partial \left( y + (1 - 2y) \times S(\vec{\theta} \cdot \vec{x}) \right)}{\partial S(\vec{\theta} \cdot \vec{x})} \cfrac{\partial S(\vec{\theta} \cdot \vec{x})}{\partial \vec{\theta}} \\ & = \cfrac{1-2y}{\partial S(\vec{\theta} \cdot \vec{x})} \cfrac{\partial S(\vec{\theta} \cdot \vec{x})}{\partial \vec{\theta}} \\ & = (1 - 2y) \times S(\vec{\theta} \cdot \vec{x}) \times \left( 1 - S(\vec{\theta} \cdot \vec{x}) \right) \cfrac{\partial \vec{\theta} \cdot \vec{x}}{\partial \vec{x}} \\ & = (1 - 2y) \times S(\vec{\theta} \cdot \vec{x}) \times \left( 1 - S(\vec{\theta} \cdot \vec{x}) \right) \vec{x} \end{align*}

Cuối cùng, hàm mất mát chỉ đơn giản là tổng của sai số của tất cả các dòng trong bảng đầu vào:

\begin{align*} \mathcal{L}(\vec{\theta}) & = \sum_{i=0}^3 erf_\vec\theta \left( \vec{x^{(i)}}, y^{(i)} \right) \\ & = \sum_{i=0}^3 \left[ y^{(i)} + (1 - 2y^{(i)}) \times S \left( \vec{\theta} \cdot \vec{x^{(i)}} \right) \right] \\ \nabla \mathcal{L}(\vec{\theta}) & = \sum_{i = 0}^3 \\ & = \sum_{i=0}^3 (1 - 2y^{(i)}) \times S \left( \vec{\theta} \cdot \vec{x^{(i)}} \right) \times \left[ 1 - S \left( \vec{\theta} \cdot \vec{x^{(i)}} \right) \right] \vec{x^{(i)}} \end{align*}

Xuống dốc

Cài đặt kỹ thuật xuống dốc trở thành đơn giản như sau:

# encoding: utf-8
import math
import random

def sigmoid(x):
    return 1.0 / (1.0 + math.exp(-x))

def dot(x, theta):
    return sum(x_i * theta_i for x_i, theta_i in zip(x, theta))

def f_prime(theta, x, y):
    s = sigmoid(dot(x, theta))
    t = (1 - 2 * y) * s * (1 - s)
    return [t * x_i for x_i in x]

def loss(theta, xs, ys):
    s = 0.0
    for i in range(len(ys)):
        x = xs[i]
        y = ys[i]
        s += y + sigmoid(dot(theta, x)) * (1 - 2 * y)
    return s

# Bảng đầu vào.
xs = (
    (1, 0, 0),
    (1, 0, 1),
    (1, 1, 0),
    (1, 1, 1),
)
ys = (0, 0, 0, 1)
# Khởi tạo theta ngẫu nhiên.
theta = [random.random() * 2 - 1 for _ in range(len(xs[0]))]
# Đinh tốc độ học.
alpha = 0.5

# Lặp xuống dốc.
for _ in range(10000):
    # Đạo hàm riêng đối với mỗi dòng đầu vào.
    grad = [f_prime(theta, x, y) for x, y in zip(xs, ys)]
    # Lấy tổng các đạo hàm riêng lại với nhau.
    grad = [sum(g[c] for g in grad) for c in range(len(xs[0]))]
    # Cập nhật theta.
    theta = [theta_i - alpha * grad_i for theta_i, grad_i in zip(theta, grad)]

# In kết quả.
print('Theta', theta)
print('Loss', loss(theta, xs, ys))
for x in xs:
    print(x[1:], 1 if sigmoid(dot(theta, x)) > 0.5 else 0)

Nếu ta chạy đoạn mã này vài lần ta sẽ nhận được một vài kết quả tương tự như:

Kết quả tốt:

('Theta', [-20.343564894829285, 13.449940134510761, 13.449940134512088])
('Loss', 0.003445503518918143)
((0, 0), 0)
((0, 1), 0)
((1, 0), 0)
((1, 1), 1)

Kết quả sai:

('Theta', [-8.775858442431886, -1.9183968394864555, -1.9398821984374943])
('Loss', 1.0001960002735877)
((0, 0), 0)
((0, 1), 0)
((1, 0), 0)
((1, 1), 0)

Khi vẽ đồ thị của kết quả đúng, biểu diễn đường \(13.45x_1 + 13.45x_2 - 20.34 = 0\)), ta sẽ thấy đường này đích thực phân chia 4 điểm đầu vào làm hai phần.

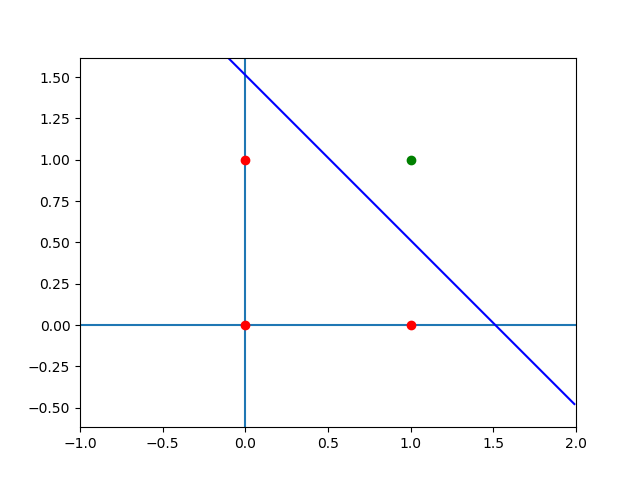
Đường thẳng phân chia 4 điểm của cổng AND

# encoding: utf-8
from matplotlib import pyplot as plt

plt.axes().set_aspect('equal', 'datalim')
plt.axvline(x=0)
plt.axhline(y=0)
plt.xlim(-1, 2)
plt.ylim(-1, 2)
plt.plot([0, 0, 1], [0, 1, 0], 'ro')
plt.plot([1], [1], 'go')
plt.plot([x / 100.0 for x in range(-10, 200)],
         [20.34 / 13.45 - x / 100.0 for x in range(-10, 200)],
         color='blue')
plt.savefig('logistic-regression-2.png')

Và nếu bạn đọc thử thay đổi số lần lặp, ví dụ như chỉ còn lặp 1000 lần, thì kết quả tốt sẽ tương tự như sau:

('Theta', [-13.21535778050865, 8.695017656986474, 8.695017826984383])
('Loss', 0.036685218920188806)
((0, 0), 0)
((0, 1), 0)
((1, 0), 0)
((1, 1), 1)

Ta nhận thấy hai điều ngoài ý muốn sau:

Kết quả không hội tụ. Mỗi lần chạy, ta có thể nhận được một kết quả khác nhau.
Có vẻ như tham số \(\vec{\theta}\) của mô hình càng tăng khi chúng ta lặp càng nhiều.

Chúng ta sẽ giải thích hai điểm này trong bài viết kế tiếp.

Tóm tắt

Trong bài viết này, chúng ta giới thiệu hàm hậu cần, nguồn gốc của cái tên "kỳ lạ" này, các đặc điểm của nó, và thiết lập hàm xích-ma chuẩn dựa theo hàm hậu cần. Kế đó, chúng ta đã giải thích khái niệm hồi quy hậu cần, đưa ra một ví dụ để từ đó xác lập phương pháp tìm tham số của mô hình. Chúng ta đã sử dụng sai số \(\vert y - \hat{y} \vert\) trong quá trình xác lập hàm mất mát. Khi áp dụng kỹ thuật xuống dốc, chúng ta gặp phải một số trục trặc khiến kết quả tìm được hoặc là không tốt, hoặc là thay đổi theo số bước xuống dốc. Bạn đọc được khuyến khích thảo luận về các vấn đề đó trong diễn đàn trước khi đọc tiếp phần sau.

Tài liệu đọc thêm

Trang Logistic function ở Wikipedia.
Trang Pierre François Verhulst ở Wikipedia.
Trang Sigmoid function ở Wikipedia.